 多面体元素ペンタドロン 
平行多面体元素 のペンタドロンを試作してみました
左右勝手対称形が１対になります
これを １２個積み上げ立方体にしたものが 下の写真です
同様に ４８個で切頂八面体
１４４個で斜六面体
１９２個で 菱形十二面体
３８４個で 長菱形十二面体 が出来ます
このページのトップへ戻る
多面体元素のつくりかた
１）まず 一辺ｍ の立方体を用意する
※素材は何でもいいけど 少し硬め以上のものが良いようです
２）対角線をカットする
３）立方体の直角の一点から 前後 左右 上下 に同様に対角線を ３回カットする
このページのトップへ戻る
４）広げると以下のようになる
５）ここからが肝心
６）写真の三角片（※名称は テトラドロンと呼びます）をすべてカットしますと以下のようになります
このページのトップへ戻る
このページのトップへ戻る
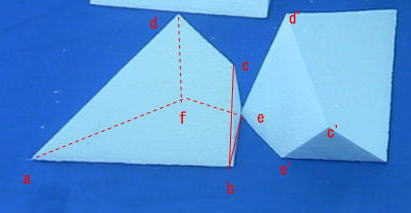
上の ｄ は ｄ’ の位置
ｃ は ｃ’ の位置に
また ｅ は ｅ’ の位置にあったもの
立方体の１辺をｍとした場合
辺ａｂ は ｍ
辺ａｄ を √３ ÷ ２ ｘ ｍ
辺ｂｃ を √２ ÷ ４ ｘｍ
辺ａｆ を ３ ｘ √２ ÷ ４ ｘ ｍ
辺ｂｅ を ｍ ÷ ２
の長さになるように ｃ ｄ ｆ ｅ の面 で カットします 出来上がるのが多面体元素ペンダトロンになるんだよ
他の三角片も 同様にして カットしていきます
※左右対称の場合は ひと工夫してね
写真のように 左右対称のペンダトロンが合計 １２個 できあがります
一旦出来上がってからばらしてしまうと、元の立方体に戻るのは至難の業になりますので
参考までに 簡単な組み立て順を ＵＰしておきます
このページのトップへ戻る
このページのトップへ戻る
１２個使って立方体の完成です
もっともっとたくさん作って 八面体や 十二面体にも挑戦してみてね
とても良い立体把握になって 頭の体操にもなるよねー
このページのトップへ戻る
トップページ ＞ 製作実例 ＞ 学校 ＞ 多面体元素ペンタドロンの試作
|
|
|
|
|
フジカット有限会社
Copyright 2002 Fujicut Co.,LTD.
All rights reserved.. |
|
｜ 
